기초 통계 정리_중심 통계량

데이터 분석의 가장 기초는 통계라고 할 수 있다. 오늘은 데이터 관점에서 중심 통계량, 변동 통계량, 형태 통계량, 관계 통계량에 대한 기초를 각각 알아보자.

 

중심 통계량

중심 통계량은 데이터의 중심경향을 나타내는 수치이다. 보통 데이터에서 결측치가 있는 경우에 데이터의 특징에 맞게 아래의 값중 골라서 NaN값 대신에 대체를 한다.

 

 

평균(Average)

표본데이터의 중심무게(산술평균, 기하평균, 조화평균, 가중평균)로 표현 할 수 있다.

 

 

산술 평균

우리가 보통 알고 있는 평균이라고 할 수 있다. 각각의 수를 모두 더한 후에 갯수로 나눠주는 것이다. 식을 보면 아래와 같다.

 

https://en.wikipedia.org/wiki/Average

 

기하 평균

산술 평균과 다르게 값들을 모두 곱한 후에 갯수로 루트를 취한다.

 

https://en.wikipedia.org/wiki/Average

 

 

조화 평균

각각의 값들의 역수에 대한 산술 평균의 역수라고 할 수 있다. 식은 아래와 같다.

 

https://en.wikipedia.org/wiki/Average

 

 

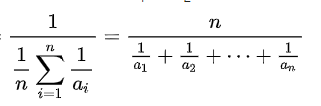
가중 평균

가중 평균은 쉽게 말해서 각각의 값들에 중요도에 따라 가중치를 주어 평균을 한 것이라고 할 수 있다.

 

https://en.wikipedia.org/wiki/Average

 

 

중앙값(Median)

중앙값은 순서대로 순위가 매겨진 그룹의 중간 숫자이다. 평균 값 대신에 중앙 값을 넣는 경우는 어느 경우 일까? 데이터가 1, 3, 5, 4, 6, 7, 9, 11,  2543456 라는 6개의 데이터가 있다고 가정해 보자. 이런 경우는 대부분의 값은 한자리 수인데, 하나만 비정상 적으로 큰 경우는 평균값을 사용하는 것보다는 중앙값을 결측치에 넣어주는 것이 좋다.

 

중앙값은 1, 3, 3, 6, 7, 8, 9의 값이 있으면, 중앙값은 6이다. 만약 1, 2, 3, 4, 5 , 6, 8, 9의 값들로 뚜렷한 중간 값이 없으면, 일반적으로 두 중간값의 평균으로 4.5를 쓰게 된다. 식으로 표현하면 아래와 같다.

 

https://en.wikipedia.org/wiki/Median

 

 

최빈값(Mode)

최빈값이란 표본데이터 중 가장 빈번한 값을 의미한다. 데이터를 다루다 보면, 범주화된 데이터에서는 가장 많은 값을 가진 범주로 NaN값을 넣어주는게 좋을 경우가 있다. 이런 경우에 최빈값을 넣어준다. 예들 들면 1, 2, 3, 3, 4, 4, 4, 4, 4, 4, 5, 6의 값이 있다면 최빈값은 4가 된다.