티스토리 뷰
회귀모델은 연속형 타겟 변수(continuous target variable)과 여러 입력 변수들(input variables)의 관계를 만드는 모델이다. 사실 f의 구조, 학습 방법에 따라 다양한 종류의 회귀모델이 존재한다.
| y = f(x1, x2, x3, ..., xp) |

적용 가능한 예로는 중고차 가격 예측, 주식 가격 예측, Object detection 등등이 있다.
Linear Regression
Linear Regression가 무엇인지 알아보자.

Regression의 핵심은 선택지가 1, 2, 3, 4번 중에 있어서 고르는 게 아니고 x값에 대한 y값이 실수로 주어지는 것이다.
ex_ 집의 평수에 따른 가격.
그리고 Regression 중에 Linear Regression이 가장 쉽다.
사실 위의 그래프를 보면, 지금 주어진 데이터를 보면 x값에 대한 y값을 다 알고 있다. 따라서 이부분은 앞에서 배운 지도 학습이라고 할 수 있다. 그리고 위와 같이 그래프 안에 선을 그릴 때 어느 선이 가장 수학적으로 정확한지를 계산할 수 있어야 한다. 그렇기 때문에 수식이 필수적으로 나온다.

위의 수식을 보면 y= ax+b 와 같이 선을 나타낼 수 있다. 여기서 a와 b를 w1과 w0으로 바꿔서 쓰는게 머신러닝의 컨벤션이다. 정리하자면, 우리가 해야할 것은 어떤 직선이 정확한지를 찾는 것, 즉 w의 값을 찾는 것이다. 데이터를 가장 잘 나타내는 w를 찾는 것이 Linear Regression 모델을 fitting 한다고 할 수 있다.
Modeling non-linear relationships
Linear Regression 이지만, 비선형도 할 수 있다.

즉, w대신에 파이(x) 라는 비선형인 함수(ex_2차 함수나 3차 식)를 넣어준다. 여기서는 많이 다루지는 않겠지만, 있다는 부분을 인지하고 있자. 이것이 Polynomial Regression이다.
Polynomial Regression 의 예
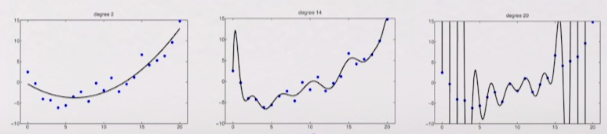
degree 1보다는 degree 2(x제곱)를 쓸 때 데이터를 잘 설명해 줄 수도 있다. 따라서 Linear Regression을 하면서 Polynomial function을 씌워서 Polynomial Regression을 하면 예측을 더 잘하는 모델이 될 수도 있다.
다중선형회귀(Multivariate linear regression)

위에서 배운 것 처럼 x가 있고 y가 있어서 2차원을 예측하는 것이 아니라, x1과 x2의 조합으로 y을 예측할 수 있다. 그랬을 때, x1의 제곱과 x2의 제곱으로 나타날 수 있다는 것이 Multivariate linear regression이다.
Maximum likelihood estimation

이 부분의 포인트는 'y = w1 x + w0'가 있을 때, 우리는 x와 y 값을 트레이닝 데이터로 알고 있다. 이러한 걸 바탕으로 w1과 w0을 어떻게 잘 찾아낼 것인가를 나타낸 수식이다.
Residual Sum of Squares
w가 적합한 선을 그어준다는것을 파악할 수 있는 가장 중요한 것이 RSS이다. 어느 선이 좋은가를 나타낸 수식이 가장 아래에 있는 RSS라고 생각하면 된다.

RSS는 w를 값을 정해서 선을 그었을 때 실제 데이터와 선분의 차이가 얼마인지를 알 수 있다. 실제 y 값과 예측된 y값의 차이라고 생각하면 된다. 이러한 방식으로 w를 찾는다. RSS 관련 그림은 아래와 같다.

Ridge Regression
선형이라 하더라도 w를 찾다보면 비선형이 들어 갈 수 있기 때문에 꽤 복잡한 선이 나올 수 있다. 이럴 경우는 fit을 너무 오버 해서 한 overfit 라고 할수 있다. 다시말하면 쓸데없이 너무 복잡한 커브가 나온다. 이러한 문제를 해결해야한다, 아래의 그림을 보면 x가 1정도 되는 곳을 보면, 하나만 튀어 올랐는데 이것은 먼가 문제가 있다는 말이다. 이렇기 때문에 Regularization을 한다. 쉽게 말하면 복잡하게 하지 말고 심플하게 한다는 말이다. 아래 그래프 옆에 적힌 숫자가 현재 그래프에서 최적의 w들의 값이다. 그런데 w값들이 크기가 너무 크다. 그래서 Regularization 입장에서는 이렇게 큰값은 선을 복잡하게 만들기 떄문에 별로 좋지 않다. 결과적으로 Ridge Regression이라는 것은 이렇게 큰 값들에 대해 패널티를 주자는 것이다.

그러면 패널티를 어떻게 줄까?



옆의 이 부분이 패널티를 주는 부분이다. 구한 w를 절대값한 후 제곱을 해서 다 더해준다. 다 저한 값이 패널티로 작용해서 더해주기 때문에, w 값 자체를 작게 만드는 w를 찾는거다. 이렇게 되면 복잡한 선이 아니고 매끄러운 선이 나온다.
아래의 그림을 보자.

왼쪽 그래프가 Ridge Regression을 안한 제일 적합한 w를 찾아낸 결과이고 오른쪽 그래프가 w의 큰 값에 대해 패널티를 준경우이다.
Regularization effects of big data
모든 머신러닝에서 Regularization이 중요하다. 위에서 '∑|w|제곱' 한 것을 'L2norm'이나 'L2Regularization' 이라고 한다. 이것을 많이 쓰기도 하지만, Regularization을 하는 다른 방법으로는 Regularization effects of big data가 있다. 이 말뜻은 데이터가 많으면 자연스럽게 regularization을 한다는 말이다. 예를들어 데이터가 5개 밖에 없으면 복잡하게 나오지만, 수백개의 데이터가 있다면 심플하게 나온다.
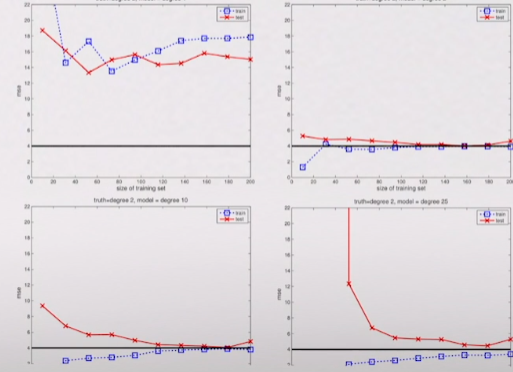
x축은 데이터의 수를 나타낸다. 그리고 빨강은 test 데이터에 대한 error고 파랑은 training 데이터에 대한 에러다. 밑에 까만선은 이상적인 error 값을 나타낸다. 학습을 할 때 적어도 training 데이터가 검정 선까지 가야한다. 못가면 모델자체가 큰 문제가 있는 것이다. 첫번째 그림의 문제는 문제를 풀 때 x제곱으로 풀어야 하는데, x로만 fitting을 하니 fitting이 전혀 안되고 있는거다.
두번째 것을 보면 둘다 x제곱으로 fitting을 한거다. test와 training도 이상적으로 가고 있다. 그런데 training error 부분이 첫번 째에서 너무 낮게 시작하는 것을 볼 수 있는데 그 말은 overfitting이 되고 있다는 걸 의미한다. 즉, 지금 training 데이터는 잘 나오는데 미래에 예측해야하는 그 test 데이터에 대해서는 에러가 크다라는 말이다. 그러나 데이터가 클 수록 갈 수록 같아지기 때문에 좋은 모델이다.
세번째를 보자. degree가 10이다.(x의 10승) 네번째는 degree가 25이다.
정리하자면 빨강과 파랑의 차이가 크면 클수록 overfitting이 크게 되고 있는거다. 세번째, 네번째도 매우 불필요한 모델을 쓰고 있지만, 데이터가 많으면 괜찮은 모델을 학습할 수 있다는 것을 알 수 있다.
'인공지능(Artificial Intelligence) > Algorithm' 카테고리의 다른 글
| django에 Yolo 넣기 (1) | 2020.09.23 |
|---|
- Total
- Today
- Yesterday
- Deque
- pandas
- error:0308010C:digital envelope routines::unsupported
- read_csv
- Express
- BFS
- 자료구조
- 클라우데라
- vuejs
- nextjs autoFocus
- useState
- django
- react autoFocus
- TensorFlow
- useHistory 안됨
- login
- nodejs
- Vue
- JavaScript
- Python
- mongoDB
- UserCreationForm
- 자연어처리
- NextJS
- DFS
- logout
- react
- typescript
- next.config.js
- Queue
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
