티스토리 뷰
직역하면 일반 최소 제곱 회귀는 하나 이상의 독립 변수와 종속 변수 간의 관계를 추정하는 통계 분석 방법이다. 관계를 추정하는 방법은 직선으로 구성된 종속 변수의 관측값과 예측값의 차이의 제곱을 합을 최소화하는 관계로 추정을 한다. 기본적으로 독립변수가 하나만 있는 모델의 직선은 아래와 같다.
Y = aX + b
위의 식은 기본적인 1차 방정식이고, 독립변수(X)와 종속변수(Y)의 관계를 적절하게 표현하는 a와 b(OLS 계수)를 찾게 된다. 찾은 식이 실제값과의 차이의 제곱을 최소화하는 식을 찾는 것이 목적이라고 할 수 있다. 기본적으로 직선으로 표현하기 때문에 종속변수(Y)를 정확하게 예측하는 것은 불가능하다. 보통 데이터가 회귀선에 얼마나 잘 맞는지는 결정계수(R^2)로 확인을 한다.
정리하면 선형회귀(직선)는 를 분석하는 방법으로 OLS를 사용한다. 그리고 이러한 과정을 OLSR이라 부른다. OLS의 LS를 풀어보면 Least Square(최소 제곱 법)이라고 한다. 최소 제곱 법의 여러 방법 중 우리는 잔차 합의 제곱을 사용한다고 위에서 언급했다. 잔차 합의 제곱은 RSS(Residual Sum of Square)라고 한다.
우선 가상의 데이터를 만들어보자. 아래의 코드에 대한 해석은 여기를 눌러서 확인하자.
def make_linear(w=0.5, b=0.8, size=50, noise=1.0):
x = np.arange(size)
y = w * x + b
noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
yy = y + noise
plt.figure(figsize=(10, 7))
plt.plot(x, y, color='r', label=f'y = {w}*x + {b}')
plt.scatter(x, yy, label='data')
plt.legend(fontsize=20)
plt.show()
print(f'w: {w}, b: {b}')
return x, yy
x, y = make_linear(size=50, w=1.1, b=0.5, noise=4)
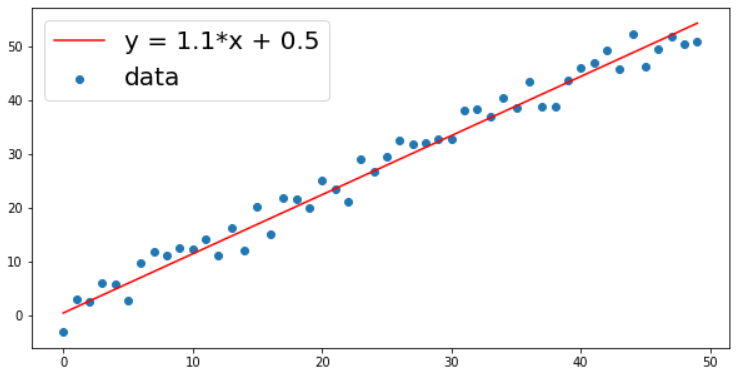
이러한 방식으로 가상의 데이터를 만들었다고 가정을 하고 아래의 값들을 분석해 보자. 파란점이 데이터고, 빨간 선이 우리가 추정하고자 하는 직선이다. 아래에서는 파란 값들을 이용해서 빨간 선을 구하는 과정이라고 이해하자.
RSS(Residual Sum Square)
실제 값(y)와 예측값(y_hat)의 차이의 제곱을 구현해 보자.
y = wx + b
라고 가정을 하면 w와 b를 구하는 식은 아래와 같다.

x_bar는 x 평균이고, y_bar는 y 평균을 나타낸다. 식을 이용해서 w와 b를 구하는 코드는 아래와 같다.
x_bar = x.mean()
y_bar = y.mean()
# w 계수
calculated_weight = ((x - x_bar) * (y - y_bar)).sum() / ((x - x_bar)**2).sum()
print('w: {:.2f}'.format(calculated_weight)) # 1.08
# b 계수
calculated_bias = y_bar - calculated_weight * x_bar
print('b: {:.2f}'.format(calculated_bias)) # 1.51
상식적으로 당연한 말이지만, outlier가 클수록 w, b의 정확한 값이 안 나온다. 즉, 최소 제곱 법은 여러 파라미터를 만들어 실습을 해보면, 노이즈에 취약하다는 점도 알 수 있을 것이다.
위의 내용은 작접 구현을 한 것이고 이제 scikit-learn을 활용해서 쉽게 구현을 해보자. LinearRegression은 최소 제곱 추정 방식으로 회귀 예측을 해주는 알고리즘이다.
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x.reshape(-1, 1), y)
> LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
print('w: {:.2f}, b: {:.2f}'.format(model.coef_[0], model.intercept_))
> w: 1.08, b: 1.51
결과로 나온 w, b를 직접구현한 것과 사이킷런을 이용한 것이 같게 나온다는 것을 확인할 수 있다.
- Total
- Today
- Yesterday
- nodejs
- read_csv
- Vue
- JavaScript
- nextjs autoFocus
- 클라우데라
- UserCreationForm
- react autoFocus
- useState
- Express
- pandas
- TensorFlow
- Python
- 자연어처리
- NextJS
- 자료구조
- vuejs
- react
- django
- Queue
- Deque
- mongoDB
- logout
- DFS
- error:0308010C:digital envelope routines::unsupported
- login
- BFS
- useHistory 안됨
- typescript
- next.config.js
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
