티스토리 뷰
머신러닝에 대한 기초적인 개념을 정리하고, 데이터를 가져와서 판다스로 전처리 후에 사이킷런을 이용하여 모델을 만들고 분석을 해볼 것이다. 출퇴근하면서 핸드폰으로 쭉 보는 것을 추천한다.
머신러닝 프로세스
머신러닝 데이터 분석을 하기 위해서 컴퓨터 알고리즘이 이해할 수 있도록 관측값(observation)을 속성(feature)기준으로 정리가 필요하다. 따라서 판다스를 이용하여 정리가 필요하다. 데이터프레임에서 열은 속성을 나타내는 변수고, 행은 하나의 관측값이다.
데이터프레임으로 정리를 했으면, 모형을 학습하기 위해 사용되어지는 훈련 데이터(train data)와, 학습이 마친 모형의 예측 능력을 평가하기 위한 검증 데이터(test data)로 나눠줘야 한다.
기본적으로 판다스에 대한 설명은 아래의 url을 참고하여 공부하고 넘어오자. 여러가지 알고리즘을 통해 분석을 시작해 보자.
회기분석(regression)
회기분석에는 기본적으로 단순회귀분석과 다항회귀분석으로 나뉜다. 회기분석에 대해 조금 더 알고 싶다면 여기를 누르자. 아래에서는 단순회귀분석, 다항회귀분석, 다중회귀분석을 사이킷런을 활용하여 구현해보자.
단순회기분석(Simple Linear Regression)
어떤 변수(독립 변수X)가 다른 변수(종속 변수Y)에 영향을 준다면 두 변수 사이에 선형 관계가 있다고 할 수 있다. 단순회기분석을 활용하면, 새로운 독립변수 X 값이 주어졌을 때 거기에 대응되는 종속 변수 Y 값을 예측이 가능하다. 우선 아래의 csv파일을 받자.
우선 데이터를 불러오자.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv('./auto-mpg.csv', header=None)
df.columns = ['mpg','cylinders','displacement','horsepower','weight',
'acceleration','model year','origin','name']
#데이터 확인 코드
print(df.head())
print(df.info())
'''
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 398 entries, 0 to 397
Data columns (total 9 columns):
mpg 398 non-null float64
cylinders 398 non-null int64
displacement 398 non-null float64
horsepower 398 non-null object
weight 398 non-null float64
acceleration 398 non-null float64
model year 398 non-null int64
origin 398 non-null int64
name 398 non-null object
dtypes: float64(4), int64(3), object(2)
memory usage: 28.1+ KB
None
'''
print(df.describe())
앞의 예제에서 봤듯, horsepower는 숫자에 '?'가 섞여있어서 object라고 뜬다. 따라서 변경해주자.
print(df['horsepower'].unique()) # horsepower 열의 고유값 확인
'''
['130.0' '165.0' '150.0' '140.0' '198.0' '220.0' '215.0' '225.0' '190.0'
'170.0' '160.0' '95.00' '97.00' '85.00' '88.00' '46.00' '87.00' '90.00'
'113.0' '200.0' '210.0' '193.0' '?' '100.0' '105.0' '175.0' '153.0'
'180.0' '110.0' '72.00' '86.00' '70.00' '76.00' '65.00' '69.00' '60.00'
'80.00' '54.00' '208.0' '155.0' '112.0' '92.00' '145.0' '137.0' '158.0'
'167.0' '94.00' '107.0' '230.0' '49.00' '75.00' '91.00' '122.0' '67.00'
'83.00' '78.00' '52.00' '61.00' '93.00' '148.0' '129.0' '96.00' '71.00'
'98.00' '115.0' '53.00' '81.00' '79.00' '120.0' '152.0' '102.0' '108.0'
'68.00' '58.00' '149.0' '89.00' '63.00' '48.00' '66.00' '139.0' '103.0'
'125.0' '133.0' '138.0' '135.0' '142.0' '77.00' '62.00' '132.0' '84.00'
'64.00' '74.00' '116.0' '82.00']
'''
df['horsepower'].replace('?', np.nan, inplace=True) # '?'을 np.nan으로 변경
df.dropna(subset=['horsepower'], axis=0, inplace=True) # 누락데이터 행을 삭제
df['horsepower'] = df['horsepower'].astype('float') # 문자열을 실수형으로 변환
# 분석에 활용할 열(속성)을 선택 (연비, 실린더, 출력, 중량)
ndf = df[['mpg', 'cylinders', 'horsepower', 'weight']]
print(ndf.head())
'''
mpg cylinders horsepower weight
0 18.0 8 130.0 3504.0
1 15.0 8 165.0 3693.0
2 18.0 8 150.0 3436.0
3 16.0 8 150.0 3433.0
4 17.0 8 140.0 3449.0
'''
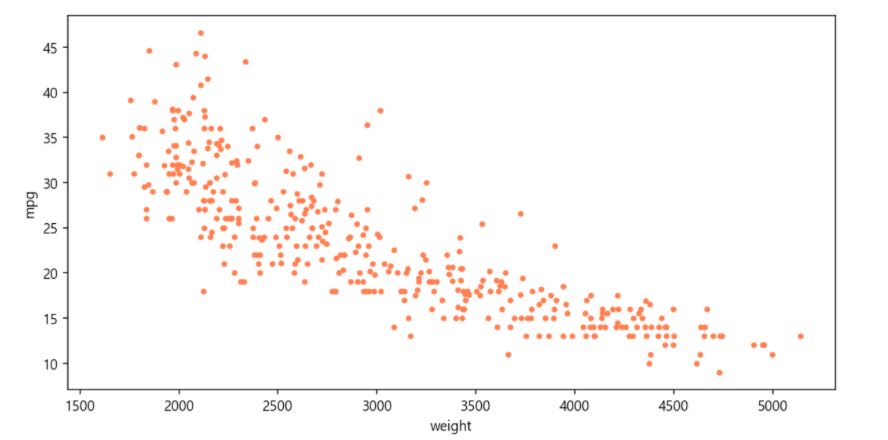
### 종속 변수 Y인 "연비(mpg)"와 다른 변수 간의 선형관계를 그래프(산점도)로 확인
# Matplotlib으로 산점도 그리기
ndf.plot(kind='scatter', x='weight', y='mpg', c='coral', s=10, figsize=(10, 5)) # 컬러, 점크기
plt.show()
plt.close()
# seaborn으로 산점도 그리기
fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
sns.regplot(x='weight', y='mpg', data=ndf, ax=ax1) # 회귀선 표시
sns.regplot(x='weight', y='mpg', data=ndf, ax=ax2, fit_reg=False) #회귀선 미표시
plt.show()
plt.close()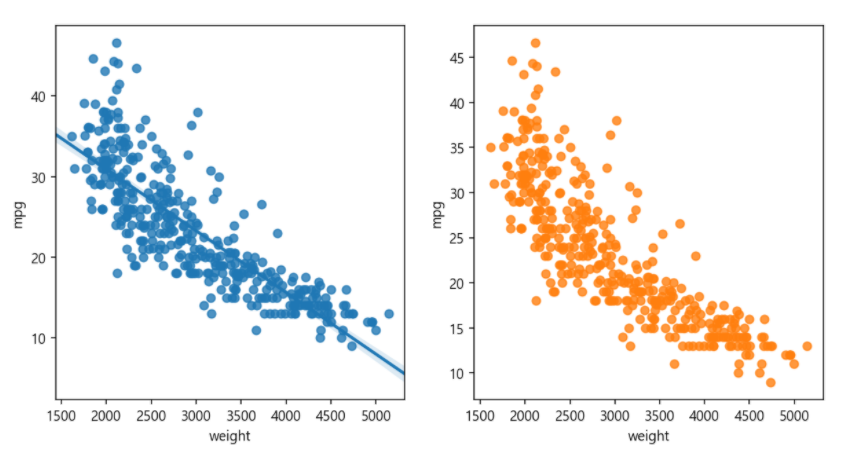
# seaborn 조인트 그래프 - 산점도, 히스토그램
sns.jointplot(x='weight', y='mpg', data=ndf) # 회귀선 없음
sns.jointplot(x='weight', y='mpg', kind='reg', data=ndf) # 회귀선 표시
plt.show()
plt.close()
# seaborn pariplot으로 두 변수 간의 모든 경우의 수 그리기
## info, describe 같은 여러개의 데이터를 한눈에 볼 수 있게 한다.
sns.pairplot(ndf)
plt.show()
plt.close()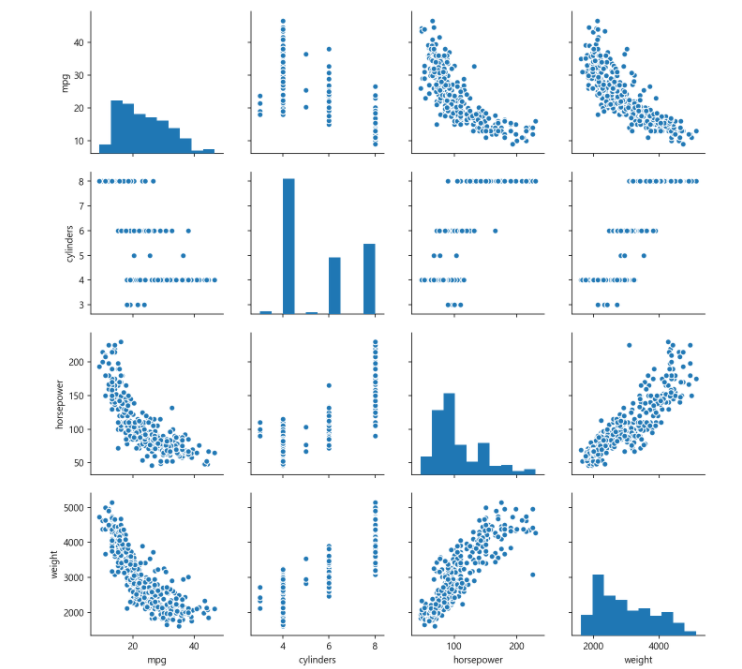
위에 부분은 사실 배웠던 내용이다.
데이터셋 구분
기본적으로 입력값(X)과 결과값(y)를 정해준다. 그 후에 사이킷런을 이용해서 train값과 test 값으로 나눠준다. 이 부분은 머신러닝 기초 부분을 확인하고 오자.
# 속성(변수) 선택
#독립 변수 X => 여러개가 뽑을 수 있으니, 시리즈로 하나하나 뽑아서 들어간다.
# 어떠한 변수를 넣든 시리즈로 계산되어 나온다.
#즉, 나중에 결과물이 나올 때 weight로 나오는 것인데, 굳이 ndf['weight']를 빼고해도 ndf[['weight']]로 해도 되긴한다.
X=ndf[['weight']]
y=ndf['mpg'] #종속 변수 Y => 하나
print(type(X))
'''
<class 'pandas.core.frame.DataFrame'>
'''
print(type(y))
'''
<class 'pandas.core.series.Series'>
'''
train_test_split함수를 활용하면 자동으로 train과 test를 나눠준다. 지도학습은 train_test_splilt를 사용한다.
# train data 와 test data로 구분(7:3 비율)
from sklearn.model_selection import train_test_split # 트레인과 테스트를 알아서 나눠죠
X_train, X_test, y_train, y_test = train_test_split(X, #독립 변수
y, #종속 변수
test_size=0.3, #검증 30% => 트레인 사이트는 70으 된다.
random_state=10) #랜덤 추출 값 -> 무자기로 10번 섞는다.
print('train data 개수: ', len(X_train))
print('test data 개수: ', len(X_test))
'''
train data 개수: 274
test data 개수: 118
'''
사이킷런을 활용하여 회귀분석 모듈(LinearRegression)을 가져와 사용할 것이다.
# sklearn 라이브러리에서 선형회귀분석 모듈 가져오기
from sklearn.linear_model import LinearRegression
# 단순회귀분석 모형 객체 생성
lr = LinearRegression()
# train data를 가지고 모형 학습
# 훈련은 fit 함수로 진행한다.
# fit함수로 모델구축할 때는 test가 아니라 train data로 한다.
lr.fit(X_train, y_train)
# 학습을 마친 모형에 test data를 적용하여 결정계수(R-제곱) 계산 / 결정계수가 높을 수록 성능이 높다.
r_square = lr.score(X_test, y_test)
print(r_square) # 성능이 얼마나 좋은지?
'''
0.6822458558299325
'''
# 회귀식의 기울기
print('기울기 a: ', lr.coef_) # Weight를 보자.
'''
기울기 a: [-0.00775343]
'''
# 회귀식의 y절편
print('y절편 b', lr.intercept_) # 절편을 보자. y절편을 가로질러서 인터셉트
'''
y절편 b 46.710366257280086
'''
# 모형에 전체 X 데이터를 입력하여 예측한 값 y_hat을 실제 값 y와 비교
y_hat = lr.predict(X) # 예측 함수. 예측해서 와이 햇을 구하자.
plt.figure(figsize=(10, 5)) # 2개 그려죠
ax1 = sns.distplot(y, hist=False, label="y") # 예측모델 넣어서 해죠.
ax2 = sns.distplot(y_hat, hist=False, label="y_hat", ax=ax1)
plt.show()
plt.close()
# 결론 보니 비선형을 선형으로 그려서 안나오네. 선형모델로 못풀겠네.
다항회기분석(Polynomial Regression)
위에서 구현해본 단순회귀분석은 두 변수 간의 관계를 직선 형태로 설명하는 알고리즘이었다. 따라서 직선보다는 곡선으로 설명하는 것이 적합할 때는 단순회귀분석 보다는 다항 함수를 사용하여 복잡한 곡선 형태의 회귀선을 표현할 수 있다. 즉 다항회귀분석은 2차함수 이상의 다항 함수를 이용하여 두 변수 간의 선형관계를 설명하는 알고리즘이다.
| Y = aX^2 +bX+c |
학습을 통해 3개의 계수 a,b,c를 찾아서 모형을 완성한다.
실습을 해보자. 위에서 겹치는 부분은 빠르게 넘어가겠다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv('./auto-mpg.csv', header=None)
df.columns = ['mpg','cylinders','displacement','horsepower','weight',
'acceleration','model year','origin','name']
df['horsepower'].replace('?', np.nan, inplace=True)
df.dropna(subset=['horsepower'], axis=0, inplace=True)
df['horsepower'] = df['horsepower'].astype('float')
ndf = df[['mpg', 'cylinders', 'horsepower', 'weight']]
X=ndf[['weight']]
y=ndf['mpg']
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)
다항회귀분석을 사용하기 위해서는 선형회귀분석에서 사용한 LinearRegression을 같게 사용하지만, PolynomialFeatures를 활용하여, 학습에서 사용하는 X값을들 이차원으로 바꾼 후에 fit에 넣어준다. 코드를 확인하다.
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures # 다항함수를 변환해준다.
# preprocessing은 전처리하겠다는 말이다.
# 전처리 중에 PolynomialFeatures은 비선형 feature에 복잡한 계산을 알아서 해준다.
poly = PolynomialFeatures(degree=2) # degree는 차원을 의미한다
X_train_poly=poly.fit_transform(X_train) # x-train을 다항식으로 변환할 수 있도록 fit_transform을 해줌
print('원 데이터: ', X_train.shape)
print('2차항 변환 데이터: ', X_train_poly.shape)
'''
원 데이터: (274, 1)
2차항 변환 데이터: (274, 3)
'''
PolynomialFeatures를 이용하여 2차항으로 변환하겠다고 지정을 한 후에 poly 객체를 만든다. 그리고 poly 객체에 fit_transform 매소드에 X_train를 전달하면 2차항 회귀분석에 맞게 변환된다. 정리하면, x_train의 1개 열이 x_train_poly에서는 3개의 열로 늘어난다.
이제 fit 메소드를 활용하여 학습을 시작해 보자.
pr = LinearRegression()
pr.fit(X_train_poly, y_train)
이제 학습을 마쳤으니, score 메소드로 모형의 결정계수(R-제곱)을 구한다. 이때 X_test도 fit_transform 매소드를 활용하여 2차항 회귀분석에 맞게 변환해야한다.
X_test_poly = poly.fit_transform(X_test)
r_square = pr.score(X_test_poly,y_test)
print(r_square)
'''
0.7087009262975685
'''
위에서 보면 70프로라는 정확도가 나온 것을 알 수 있다.
이제 train data의 산점도와 test data로 예측한 회귀선을 그래프로 출력해 보자. y_hat_test의 산점도와 test data로 예측한 회귀선을 그래프로 출력하자. predict() 메소드에 입력하여 예측한 결과인 y_hat_test를 빤간 점으로 표시하면 회귀선이 된다.
y_hat_test = pr.predict(X_test_poly)
fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(1, 1, 1)
ax.plot(X_train, y_train, 'o', label='Train Data')
ax.plot(X_test, y_hat_test, 'r+', label='Predicted Value')
ax.legend(loc='best') # loc는 최고에다가 알아서 찍어죠.
plt.xlabel('weight')
plt.ylabel('mpg')
plt.show()
plt.close()
이제 실제 값과 예측 값을 비교해 보자. Seaborn 라이브러리의 distplot() 함수를 사용하여 실제 값 y와 d예측값 y_hat의 분포 차이를 비교한다.
X_ploy = poly.fit_transform(X)
y_hat = pr.predict(X_ploy)
plt.figure(figsize=(10, 5))
ax1 = sns.distplot(y, hist=False, label="y")
ax2 = sns.distplot(y_hat, hist=False, label="y_hat", ax=ax1)
plt.show()
plt.close()
단순 회기분석의 결과와 비교할 때 데이터가 어느한 쪽으로 편향되는 경향이 감소한 것을 보면, 더 적합한 모형이라고 할 수 있다.
다중회귀분석(Multivariate Regression)
여러 개의 독립 변수가 종속 변수에 영향을 주고 선형 관계를 갖는 경우를 다중회귀분석이라 한다. 우선은 위랑 동일한 코드를 우선 작성해 보자.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv('./auto-mpg.csv', header=None)
df.columns = ['mpg','cylinders','displacement','horsepower','weight',
'acceleration','model year','origin','name']
df['horsepower'].replace('?', np.nan, inplace=True)
df.dropna(subset=['horsepower'], axis=0, inplace=True)
df['horsepower'] = df['horsepower'].astype('float')
ndf = df[['mpg', 'cylinders', 'horsepower', 'weight']]
아래와 같이 X 값에는 독립변수 3개를 넣고 data를 구분해 주자.
X=ndf[['cylinders', 'horsepower', 'weight']] # 독립변수
y=ndf['mpg'] # 종속 변수
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)
print('훈련 데이터: ', X_train.shape)
print('검증 데이터: ', X_test.shape)
'''
훈련 데이터: (274, 3)
검증 데이터: (118, 3)
'''
이 후에는 LinearRegression() 함수를 사용하여 회귀분석 모형 객체를 생성하고 앞에서 진행한 부분과 동일하게 진행한다.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train, y_train)
r_square = lr.score(X_test, y_test)
print(r_square) # 결정계수
'''
0.6939048496695599
'''
print('X 변수의 계수 a: ', lr.coef_)
'''
X 변수의 계수 a: [-0.60691288 -0.03714088 -0.00522268]
'''
print('상수항 b', lr.intercept_)
'''
상수항 b 46.414351269634025
'''
y_hat = lr.predict(X_test)
plt.figure(figsize=(10, 5))
ax1 = sns.distplot(y_test, hist=False, label="y_test")
ax2 = sns.distplot(y_hat, hist=False, label="y_hat", ax=ax1)
plt.show()
plt.close()

그래프를 보면 한쪽으로 편향되는 경향은 그대로 남아 있지만 그래프의 첨도(뾰족한 정도)가 약간 누그러진 것을 볼 수 있다.
분류(classification)
분류는 대상의 속성을 입력 받고, 목표 변수가 갖고 있는 케테고리(범주형) 값 중에서 분류하여 예측한다. 목표 변수 값을 함께 입력하기 때문에 지도 학습 유형에 속하는 알고리즘이다. KNN, SVM, Decision Tree, Logistic Regression 등의 알고리즘이 존재한다.
KNN(k-Nearest-Neighbors)
KNN은 k개의 가까운 이웃이라는 뜻이다. 관측값이 주어지면 관측값을 기준으로 가까운 순서로 k개의 속성을 찾고, 가장 많은 속성으로 분류한다. 이때 k값에 따라 정확도가 달라지므로 적절한 k값을 찾는 것이 매우 중요하다.
데이터는 Seaborn 라이브러리에서 'titanic' 데이터셋을 활용한다. 이전 블로그에서 다뤘으므로 데이터에 설명은 생락한다.
import pandas as pd
import seaborn as sns
df = sns.load_dataset('titanic')
print(df.head())
'''
survived pclass sex age sibsp parch fare embarked class \
0 0 3 male 22.0 1 0 7.2500 S Third
1 1 1 female 38.0 1 0 71.2833 C First
2 1 3 female 26.0 0 0 7.9250 S Third
3 1 1 female 35.0 1 0 53.1000 S First
4 0 3 male 35.0 0 0 8.0500 S Third
who adult_male deck embark_town alive alone
0 man True NaN Southampton no False
1 woman False C Cherbourg yes False
2 woman False NaN Southampton yes True
3 woman False C Southampton yes False
4 man True NaN Southampton no True
'''
print(df.info())
'''
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 15 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 survived 891 non-null int64
1 pclass 891 non-null int64
2 sex 891 non-null object
3 age 714 non-null float64
4 sibsp 891 non-null int64
5 parch 891 non-null int64
6 fare 891 non-null float64
7 embarked 889 non-null object
8 class 891 non-null category
9 who 891 non-null object
10 adult_male 891 non-null bool
11 deck 203 non-null category
12 embark_town 889 non-null object
13 alive 891 non-null object
14 alone 891 non-null bool
dtypes: bool(2), category(2), float64(2), int64(4), object(5)
memory usage: 80.6+ KB
None
'''
데이터에서 NaN값이 많은 열을 삭제하고 전처리를 진행하자.
rdf = df.drop(['deck', 'embark_town'], axis=1) # axis=1 열 기준 연산
print(rdf.columns.values)
'''
['survived' 'pclass' 'sex' 'age' 'sibsp' 'parch' 'fare' 'embarked' 'class'
'who' 'adult_male' 'alive' 'alone']
'''
rdf = rdf.dropna(subset=['age'], how='any', axis=0)
most_freq = rdf['embarked'].value_counts(dropna=True).idxmax() # print(rdf.describe(include='all'))
rdf['embarked'].fillna(most_freq, inplace=True)
분석에 사용할 속성을 지정하고, get_dummies를 활용하여 원핫인코딩을 적용하고 prefix 옵션을 사용하여 접두어를 붙여주자.
ndf = rdf[['survived', 'pclass', 'sex', 'age', 'sibsp', 'parch', 'embarked']]
onehot_sex = pd.get_dummies(ndf['sex'])
ndf = pd.concat([ndf, onehot_sex], axis=1)
onehot_embarked = pd.get_dummies(ndf['embarked'], prefix='town')
ndf = pd.concat([ndf, onehot_embarked], axis=1)
ndf.drop(['sex', 'embarked'], axis=1, inplace=True)
독립변수를 지정하고 StandardScaler()preprocessing.StandardScaler().fit(X).transform(X)을 활용하여 데이터의 상대적 크기 차이를 없애기 위하여 데이터 정규화(normalization)을 진행한다.
X=ndf[['pclass', 'age', 'sibsp', 'parch', 'female', 'male',
'town_C', 'town_Q', 'town_S']] #독립 변수 X
y=ndf['survived']
from sklearn import preprocessing
X = preprocessing.StandardScaler().fit(X).transform(X) # standardScaler => 통계화 시킴.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)
사이킷런에서 KNeighborsClassifier를 통해 KNN 분류 모형을 가져오자. 이때 k값을 넣어준다. 비지도라 k값은 알 수가 없고 여러개 해보고 제일 좋은 것을 선택한다. 그리고 학습을 진행하고 예측값과 결과값을 비교해 보자.
from sklearn.neighbors import KNeighborsClassifier # 최근접 분류모델을 쓴다.
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)
y_hat = knn.predict(X_test)
print(y_hat[0:10])
print(y_test.values[0:10])
'''
[0 0 1 0 0 1 1 1 0 0]
[0 0 1 0 0 1 1 1 0 0]
'''
모형의 예측 능력을 평가해 보자. metrics 모듈의 confusion_matrix() 함수를 사용하여 Confusion Matrix를 계산하자. 그리고 classification_report() 함수를 사용하여 precision, recall, f1-score 지표를 출력해 준다. 관련 개념은 코드 아래부분을 참고하자.
from sklearn import metrics
knn_matrix = metrics.confusion_matrix(y_test, y_hat) # 메트릭스 => 평가 측정 지표...
print(knn_matrix)
knn_report = metrics.classification_report(y_test, y_hat) # 정리해서 도출되기 때문에 R보다 좋다
print(knn_report) # confusion_matrix는 헷갈리고 시험도 많이 나온다.
'''
[[109 16]
[ 25 65]]
precision recall f1-score support
0 0.81 0.87 0.84 125
1 0.80 0.72 0.76 90
avg / total 0.81 0.81 0.81 215
'''
위의 내용에 대한 설명은 아래와 같다.
분류 모형의 예측력을 평가하는 지표
1. Confusion Matrix
모형을 예측하는 값에는 True와 False가 있다. 그리고 아래의 그림과 같이 모형의 예측값과 실제 값을 각각 축으로 하는 2x2 매트릭스로 표현한 것을 Confusion Matrix라고 부른다.
| T 예측값 F |
TP (True Positive) |
FP (False Positive) |
|
FN (False Negative) |
TN (True Negative) |
||
T F 실제값 |
|||
2. 정확도(Precision)
True로 예측한 분석대상 중에서 실제 값이 True인 비율을 말하며, 모형의 정확성을 나타내는 지표가 된다. 정확도가 높다는 것은 False Positive(실제 False를 True로 잘못 예측) 오류가 적다는 말이다.
| Precision = TP / (TP+FP) |
3. 재현율(Recall)
실제 값이 True인 분석대상 중에서 True로 예측하여 모형이 적중한 비율을 말하며, 모형의 완전성을 나타내는 지표이다. 재현율이 높다는 것은 False Negative(실제 True를 False로 잘못 예측) 오류가 낮다는 뜻이다.
| Recall = TP / (TP+FN) |
4. F1 지표(F1-score)
정확도와 재현율이 균등하게 반영될 수 있도록 정확도와 재현율의 조화평균을 계산한 값으로, 모형의 예측력을 종합적으로 평가하는 지표이다. 값이 높을수록 분류 모형의 예측력이 좋다고 말할 수 있다.
| F1 score = 2* ( Precision * Recall ) / ( Precision + Recall ) |
SVM(Support Vector Machine)
분류모델 중 하나로 벡터(vector) 개념을 가져와서 사용한다. 데이터프레임의 각 열이 고유의 축을 가지는 벡터공간을 만들고, 각각의 개별의 모든 속성이 축의 좌표로 표시되어 벡터 공간에서 위치를 나타낸다. 속성(열)이 2개가 존재하면 2차원, 4개가 존재하면 4차원 평면 공간에 데이터 셋이 좌표로 표시된다.
같은 분류 값인 데이터끼리 같은 공간에 위치시켜 벡터 공간을 여러 조각으로 나누고, 새로운 데이터에 대하여 어느 공간에 위치하는지 분류할 수 있게 한다.
위에서 반복되는 코드는 빠르게 넘어가 보자.
import pandas as pd
import seaborn as sns
df = sns.load_dataset('titanic')
# NaN값이 많은 deck 열을 삭제, embarked와 내용이 겹치는 embark_town 열을 삭제
rdf = df.drop(['deck', 'embark_town'], axis=1)
# age 열에 나이 데이터가 없는 모든 행을 삭제 - age 열(891개 중 177개의 NaN 값)
rdf = rdf.dropna(subset=['age'], how='any', axis=0)
# embarked 열의 NaN값을 승선도시 중에서 가장 많이 출현한 값으로 치환하기
most_freq = rdf['embarked'].value_counts(dropna=True).idxmax()
rdf['embarked'].fillna(most_freq, inplace=True)
ndf = rdf[['survived', 'pclass', 'sex', 'age', 'sibsp', 'parch', 'embarked']]
onehot_sex = pd.get_dummies(ndf['sex'])
ndf = pd.concat([ndf, onehot_sex], axis=1)
onehot_embarked = pd.get_dummies(ndf['embarked'], prefix='town')
ndf = pd.concat([ndf, onehot_embarked], axis=1)
ndf.drop(['sex', 'embarked'], axis=1, inplace=True)
X=ndf[['pclass', 'age', 'sibsp', 'parch', 'female', 'male',
'town_C', 'town_Q', 'town_S']] #독립 변수 X
y=ndf['survived'] #종속 변수 Y
from sklearn import preprocessing
X = preprocessing.StandardScaler().fit(X).transform(X)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)
사이킷런에서 svm을 불러과서 구현을 해주자. 이때 kernel='rbf'를 넣어주자. 안 넣어주면 에러가 뜬다.
from sklearn import svm
# kernel 이란? 데이터를 벡터 공간으로 매핑하는 함수
# rbf : radial basis function
svm_model = svm.SVC(kernel='rbf')
svm_model.fit(X_train, y_train)
y_hat = svm_model.predict(X_test)
print(y_hat[0:10])
print(y_test.values[0:10])
'''
[0 0 1 0 0 0 1 0 0 0]
[0 0 1 0 0 1 1 1 0 0]
'''
위의 결과를 보면 첫 10개 데이터 중에서 8개만 일치한다. 이제 모형의 예측 능력을 지표로 뽑아보자.
### True False 문제이기 때문에 분류문제는 confusion_matrix를 쓴다. ###
from sklearn import metrics
svm_matrix = metrics.confusion_matrix(y_test, y_hat)
print(svm_matrix)
'''
[[120 5]
[ 35 55]]
'''
svm_report = metrics.classification_report(y_test, y_hat)
print(svm_report)
'''
precision recall f1-score support
0 0.77 0.96 0.86 125
1 0.92 0.61 0.73 90
accuracy 0.81 215
macro avg 0.85 0.79 0.80 215
weighted avg 0.83 0.81 0.81 215
'''
confusion_matrix를 보면 215명의 승객 중에서 미생존자를 정확히 예측한 TP는 120명, 미생존자를 생존자로 잘못 분류한 FP는 5명, 생존자를 미생존자로 잘못 분류한 FN은 35명, 생존자를 정확하게 예측한 TN은 55명이다. 이때, 미생존자는 0의 값을 가져 False고, 생존자가 1의 값을 가져서 True가 되어 confusion_matrix를 계산한 것이다.
classification_report() 함수로 출력된 precision, recall, f1-score 지표를 보자. f1-score 지표를 보면 미생존자(0) 예측의 정확도가 0.86이고, 생존자(1) 예측의 정확도는 0.73으로 예측 능력에 차이가 있다. 사실 KNN 모형과 예측 능력에는 큰 차이가 없다.
의사결정 나무 (Decision Tree)
컴퓨터 알고리즘에서 즐겨 사용하는 트리(tree) 구조를 사용하고, 각 분기점(node)에는 목표 값을 가장 잘 분류할 수 있는 분석대상의 속성(설명 변수)들이 위치한다.
각각의 분기점에서 최적 속성을 선택 시 속성을 기준으로 분류한 값들이 구분되는 정도를 측정한다. 이 때 Entropy를 주로 활용하는데, Entropy가 낮을수록 분류가 잘 된 것이고, Entropy가 일정 수준 이하로 낮아질 때까지 앞의 과정을 반복한다. 즉, 각 분기점에서 최적의 속성을 찾기 위해 분류 정도를 평가하는 기준이 entropy이다.
바로 코드를 보자.
import pandas as pd
import numpy as np
# Breast Cancer 데이터셋 가져오기 (출처: UCI ML Repository)
uci_path = 'https://archive.ics.uci.edu/ml/machine-learning-databases/\
breast-cancer-wisconsin/breast-cancer-wisconsin.data'
df = pd.read_csv(uci_path, header=None)
df.columns = ['id','clump','cell_size','cell_shape', 'adhesion','epithlial',
'bare_nuclei','chromatin','normal_nucleoli', 'mitoses', 'class']
print(df.head())
'''
id clump cell_size cell_shape adhesion epithlial bare_nuclei \
0 1000025 5 1 1 1 2 1
1 1002945 5 4 4 5 7 10
2 1015425 3 1 1 1 2 2
3 1016277 6 8 8 1 3 4
4 1017023 4 1 1 3 2 1
chromatin normal_nucleoli mitoses class
0 3 1 1 2
1 3 2 1 2
2 3 1 1 2
3 3 7 1 2
4 3 1 1 2
'''
print(df.info())
'''
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 699 entries, 0 to 698
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 id 699 non-null int64
1 clump 699 non-null int64
2 cell_size 699 non-null int64
3 cell_shape 699 non-null int64
4 adhesion 699 non-null int64
5 epithlial 699 non-null int64
6 bare_nuclei 699 non-null object
7 chromatin 699 non-null int64
8 normal_nucleoli 699 non-null int64
9 mitoses 699 non-null int64
10 class 699 non-null int64
dtypes: int64(10), object(1)
memory usage: 60.2+ KB
None
'''
print(df.describe())
'''
id clump cell_size cell_shape adhesion \
count 6.990000e+02 699.000000 699.000000 699.000000 699.000000
mean 1.071704e+06 4.417740 3.134478 3.207439 2.806867
std 6.170957e+05 2.815741 3.051459 2.971913 2.855379
min 6.163400e+04 1.000000 1.000000 1.000000 1.000000
25% 8.706885e+05 2.000000 1.000000 1.000000 1.000000
50% 1.171710e+06 4.000000 1.000000 1.000000 1.000000
75% 1.238298e+06 6.000000 5.000000 5.000000 4.000000
max 1.345435e+07 10.000000 10.000000 10.000000 10.000000
epithlial chromatin normal_nucleoli mitoses class
count 699.000000 699.000000 699.000000 699.000000 699.000000
mean 3.216023 3.437768 2.866953 1.589413 2.689557
std 2.214300 2.438364 3.053634 1.715078 0.951273
min 1.000000 1.000000 1.000000 1.000000 2.000000
25% 2.000000 2.000000 1.000000 1.000000 2.000000
50% 2.000000 3.000000 1.000000 1.000000 2.000000
75% 4.000000 5.000000 4.000000 1.000000 4.000000
max 10.000000 10.000000 10.000000 10.000000 4.000000
'''
위의 값을 보면 'bare_nuclei' 열을 제외한 나머지 열은 모두 숫자다. unique() 를 이용해서 확인해 보고 replace와 dropna를 이용해서 누락행을 지워보자.
print(df['bare_nuclei'].unique())
'''
['1' '10' '2' '4' '3' '9' '7' '?' '5' '8' '6']
'''
df['bare_nuclei'].replace('?', np.nan, inplace=True)
df.dropna(subset=['bare_nuclei'], axis=0, inplace=True)
df['bare_nuclei'] = df['bare_nuclei'].astype('int')
이제 설명 변수 X와 예측 변수로 사용할 열을 분리한다. 그 후에 설명 변수를 정규화(서로 다른 데이터 값들을 모음)하고 훈련 데이터와 검증 데이터를 분리한다.
X=df[['clump','cell_size','cell_shape', 'adhesion','epithlial',
'bare_nuclei','chromatin','normal_nucleoli', 'mitoses']] #설명 변수 X
y=df['class']
from sklearn import preprocessing
X = preprocessing.StandardScaler().fit(X).transform(X)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)
이제 DecisionTreeClassifier() 함수를 사용하여 모형 객체를 생성하자. 각 분기점에서 최적의 속성을 찾기 위한 평가 기준으로 'entropy' 값을 사용한다. 그리고 'max_depth'으로 트리 레벨을 지정가능하다. 아래처럼 5로 지정을 하면 5단계까지 가지를 확장할 수 있어진다. 레벨이 많아 질수록 예측은 정확해지지만, 너무 많은 트리는 훈련과정에서 train_data에만 지나치게 최적화되어 실제 데이터 예측 능력이 떨어진다. 따라서 적정한 레벨값을 찾는 것이 중요하다.
그리고 fit() 으로 모형을 학습시키고, predict() 매소드에 검증 데이터(x_test)를 전달하여 예측된 결과를 y_hat에 저장한다.
from sklearn import tree
tree_model = tree.DecisionTreeClassifier(criterion='entropy', max_depth=5) # 5단계까지 가지 확장
tree_model.fit(X_train, y_train)
y_hat = tree_model.predict(X_test) # 2: benign(양성), 4: malignant(악성)
print(y_hat[0:10])
print(y_test.values[0:10])
'''
[4 4 4 4 4 4 2 2 4 4]
[4 4 4 4 4 4 2 2 4 4]
'''
성능 평가를 통해 Confusion Matrix를 계산해보자.
from sklearn import metrics
tree_matrix = metrics.confusion_matrix(y_test, y_hat)
print(tree_matrix)
'''
[[127 4]
[ 2 72]]
'''
tree_report = metrics.classification_report(y_test, y_hat)
print(tree_report)
'''
precision recall f1-score support
2 0.98 0.97 0.98 131
4 0.95 0.97 0.96 74
accuracy 0.97 205
macro avg 0.97 0.97 0.97 205
weighted avg 0.97 0.97 0.97 205
'''
Confusion Matrix를 보면 양성을 정확히 예측한 TP는 127개, 양성을 악성으로 잘못 분류한 FP는 4개, 악성을 양성으로 잘못 분류한 FN은 2개, 악성을 정확하게 예측한 TN은 72개이다. f1-csore 지표를 보면 양성 종량(2) 예측 정확도가 0.98이고, 악성 종양(4) 예측의 정확도는 0.96으로 예측 능력에 큰 차이가 없다. 평균적으로 0.97의 정확도를 가진다고 볼 수 있다.
군집(clustering)
군집 분석은 비지도학습 유형으로 데이터셋의 관측값이 갖고 있는 여러 속성을 분석하여 서로 비슷한 특징을 갖는 관측값끼리 같은 클러스트(집단)로 묶는 알고리즘이다. 각각의 클러스트는 서로 완전하게 구분되는 특징을 가지기 때문에 어느 클러스트에도 속하지 못하는 관측값이 존재할 수 있다. 따라서 이런 특성을 이용하여 특이 데이터(이상값, 중복값 등)을 찾는데 활용되기도 한다.
비지도학습이기 때문에 군집 분석은 정답이 없는 상태에서 데이터 자체의 유사성만을 기준으로 판단한다. 군집 알고리즘은 신용카드 부정 사용 탐지, 구매 패턴 분석 등 소비자 행동 특성을 그룹화 하는데 사용된다. 어떤 소비자와 유사한 특성을 갖는 집단을 구분하게 되면, 새로운 소비자의 구매 패턴이나 행동 등을 예측하는데 활용할 수 있다. 여기서는 k-means 알고리즘과 DBSCAN 알고리즘에 대해 알아보자.
k-Means
데이터 간의 유사성을 측정하는 기준으로 각 클러스터의 중심까지의 거리를 이용한다. k개의 클러스터가 주어진다면, 각각의 클러스터에서 거리가 가까운 클러스터로 해당 데이터를 할당한다. 그리고 클러스트는 완전한 구분을 위해서 일정한 거리 이상 떨어져야 한다. k 값이 클수록 일반적으로 모형의 정확도는 개선이 되지만, 너무 커지면 선택지가 많아지기 때문에 분석의 효과가 떨어진다.
데이터는 UCI ML Repository의 도매업 고객(wholesale customers) 데이터 셋을 사용한다. URL을 입력하여 다운받아서 실습을 해보자. 'Channel' 열은 호텔/레스토랑 또는 소매점 등 판매채너러 값이고, 'Region' 열은 고객 소재지를 나타낸다.
import pandas as pd
import matplotlib.pyplot as plt
uci_path = 'https://archive.ics.uci.edu/ml/machine-learning-databases/\
00292/Wholesale%20customers%20data.csv'
df = pd.read_csv(uci_path, header=0)
print(df.head())
'''
Channel Region Fresh Milk Grocery Frozen Detergents_Paper Delicassen
0 2 3 12669 9656 7561 214 2674 1338
1 2 3 7057 9810 9568 1762 3293 1776
2 2 3 6353 8808 7684 2405 3516 7844
3 1 3 13265 1196 4221 6404 507 1788
4 2 3 22615 5410 7198 3915 1777 5185
'''
print(df.info())
'''
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 440 entries, 0 to 439
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Channel 440 non-null int64
1 Region 440 non-null int64
2 Fresh 440 non-null int64
3 Milk 440 non-null int64
4 Grocery 440 non-null int64
5 Frozen 440 non-null int64
6 Detergents_Paper 440 non-null int64
7 Delicassen 440 non-null int64
dtypes: int64(8)
memory usage: 27.6 KB
None
'''
print(df.describe())
'''
Channel Region Fresh Milk Grocery \
count 440.000000 440.000000 440.000000 440.000000 440.000000
mean 1.322727 2.543182 12000.297727 5796.265909 7951.277273
std 0.468052 0.774272 12647.328865 7380.377175 9503.162829
min 1.000000 1.000000 3.000000 55.000000 3.000000
25% 1.000000 2.000000 3127.750000 1533.000000 2153.000000
50% 1.000000 3.000000 8504.000000 3627.000000 4755.500000
75% 2.000000 3.000000 16933.750000 7190.250000 10655.750000
max 2.000000 3.000000 112151.000000 73498.000000 92780.000000
Frozen Detergents_Paper Delicassen
count 440.000000 440.000000 440.000000
mean 3071.931818 2881.493182 1524.870455
std 4854.673333 4767.854448 2820.105937
min 25.000000 3.000000 3.000000
25% 742.250000 256.750000 408.250000
50% 1526.000000 816.500000 965.500000
75% 3554.250000 3922.000000 1820.250000
max 60869.000000 40827.000000 47943.000000
'''
비지도 학습 모형이므로 예측 변수를 지정할 필요가 없고 필요한 속성을 모두 설명 변수로 활용한다. StandardScaler() 함수 등을 이용하여 학습 데이터를 정규화하여 상대적 크기 차이를 줄여준다.
X = df.iloc[:, :]
from sklearn import preprocessing
X = preprocessing.StandardScaler().fit(X).transform(X)
print(X[:5])
'''
[[ 1.44865163 0.59066829 0.05293319 0.52356777 -0.04111489 -0.58936716
-0.04356873 -0.06633906]
[ 1.44865163 0.59066829 -0.39130197 0.54445767 0.17031835 -0.27013618
0.08640684 0.08915105]
[ 1.44865163 0.59066829 -0.44702926 0.40853771 -0.0281571 -0.13753572
0.13323164 2.24329255]
[-0.69029709 0.59066829 0.10011141 -0.62401993 -0.3929769 0.6871443
-0.49858822 0.09341105]
[ 1.44865163 0.59066829 0.84023948 -0.05239645 -0.07935618 0.17385884
-0.23191782 1.29934689]]
'''
사이킷런에서 cluster 무듈을 import 한다. 그리고 KMeans() 함수로 모형 객체를 생성하는데 n_clusters 옵션을 사용하여 클러스터 개수를 5로 지정해 주잔 후에 fit()으로 학습을 하자.
from sklearn import cluster
kmeans = cluster.KMeans(init='k-means++', n_clusters=5, n_init=10) # 클러스터 개수: 5개
cluster.KMeans()
kmeans.fit(X)
cluster_label = kmeans.labels_
print(cluster_label)
'''
[1 1 1 2 1 1 1 1 2 1 1 1 1 1 1 2 1 2 1 2 1 2 2 0 1 1 2 2 1 2 2 2 2 2 2 1 2
1 1 2 2 2 1 1 1 1 1 3 1 1 2 2 1 1 2 2 3 1 2 2 1 3 1 1 2 3 2 1 2 2 2 0 2 1
1 2 2 1 2 2 2 1 1 2 1 3 3 0 2 2 2 2 3 0 1 2 1 2 2 2 1 1 1 0 2 2 1 1 1 1 2
1 2 2 2 2 2 2 2 2 2 2 2 1 2 0 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2
2 2 2 2 2 2 2 1 1 2 1 1 1 2 2 1 1 1 1 2 2 2 1 1 2 1 2 1 2 2 2 2 2 0 2 0 2
2 2 2 1 1 2 2 2 1 2 2 4 1 4 4 1 1 4 4 4 1 4 4 4 1 4 3 4 4 1 4 1 4 1 4 4 4
4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 1 4 4 4 4 4 3 4 4 4 4 4 4 4
4 4 4 4 4 1 4 1 4 1 4 4 4 4 2 2 2 2 2 2 1 2 1 2 2 0 2 2 2 2 2 2 2 2 1 4 1
4 1 1 4 1 1 1 1 1 1 1 4 4 1 4 4 1 4 4 1 4 4 4 1 4 4 4 4 4 0 4 4 4 4 4 1 4
3 4 1 4 4 4 4 1 1 2 1 2 2 1 1 2 1 2 1 2 1 2 2 2 1 2 2 2 2 2 2 2 1 2 2 2 2
1 2 2 1 2 2 1 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2
1 1 2 2 2 2 2 2 1 1 2 1 2 2 1 2 1 1 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2]
'''
df['Cluster'] = cluster_label
위의 결과를 보면 모형은 8개의 속성을 활용하여 관측값을 5개의 클러스터로 구분하여 준다. 이제 그래프를 그려보자. 8개의 변수를 하나의 그래프로 표현할 수 없어서 2개의 변수한 선택해서 해보자.
df.plot(kind='scatter', x='Grocery', y='Frozen', c='Cluster', cmap='Set1',
colorbar=False, figsize=(10, 10))
df.plot(kind='scatter', x='Milk', y='Delicassen', c='Cluster', cmap='Set1',
colorbar=True, figsize=(10, 10))
plt.show()
plt.close()
그래프를 보면 자나치게 큰 값으로 구성되는 클러스터인 라벨이 0과 4를 제외하고 1, 2, 3에 속하는 데이터만으로 다시 그려보자.
mask = (df['Cluster'] == 0) | (df['Cluster'] == 4)
ndf = df[~mask] # not
ndf.plot(kind='scatter', x='Grocery', y='Frozen', c='Cluster', cmap='Set1',
colorbar=False, figsize=(5, 5))
ndf.plot(kind='scatter', x='Milk', y='Delicassen', c='Cluster', cmap='Set1',
colorbar=True, figsize=(5, 5))
plt.show()
plt.close()
'인공지능(Artificial Intelligence) > 머신러닝' 카테고리의 다른 글
| AI_머신러닝 기초 정리 (0) | 2021.04.20 |
|---|---|
| 로지스틱 회귀(Logistic Regression) 기초 정리 (0) | 2021.01.29 |
| [머신러닝] 확률 기초정리 (0) | 2021.01.21 |
- Total
- Today
- Yesterday
- 자료구조
- Deque
- react
- logout
- NextJS
- 클라우데라
- JavaScript
- useState
- nodejs
- BFS
- pandas
- useHistory 안됨
- 자연어처리
- vuejs
- Python
- read_csv
- Vue
- django
- mongoDB
- nextjs autoFocus
- next.config.js
- DFS
- react autoFocus
- Queue
- typescript
- Express
- error:0308010C:digital envelope routines::unsupported
- UserCreationForm
- login
- TensorFlow
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
