티스토리 뷰
0, 들어가면서
손실 함수란 신경망이 학습 시 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 하는지를 알 수 있는 지표이다. 즉, 손실함수의 결과값을 가장 작게 만드는 가중치 매개변수를 찾아야 한다. 어떻게 찾는지 알아보자.
1. 데이터 학습
머신러닝에서 가장 중요한 것은 무엇일까? 바로 데이터다. 데이터를 통해 패턴을 찾고 그 패턴을 통해 특징을 추출한다. 특징이란 데이터 중에 본질적이고 중요한 데이터를 선별하는 것이고, 선별된 특징으로 패턴을 머신러닝(기계학습)하는 것이다. 이때 이미지의 특징은 보통 벡터로 표현되는데, 컴퓨터 비전 분야에서는 SIFT, SURF, HOG 등의 특징을 사용한다. 이런 특징을 사용하여 이미지 데이터를 벡터로 변환하다. 변환 후에는 지도학습의 대표 분류법인 SVM, KNN등으로 학습을 할 수 있다. 즉, 수집된 데이터를 통해 규칙을 찾아내는 것이 기계가 하는 일이라고 할 수 있다. 그러나 여기서는 특징 자체를 사람이 설계하게 된다. 다시 정리해 보면 이미지 데이터에서 특징을 추출하고 결과를 내는 방식은 아래 3가지로 나눌 수 있다.
- 이미지 => 사람에 의해 만들어진 알고리즘 => 결과
- 이미지 => 사람이 생각한 특징(FIFT, HOG 등) => 기계학습(SVM, KNN 등) => 결과
- 이미지 => Deep Learning(신경망) => 결과
3번의 경우, 신경망은 데이터를 그대로 학습한다. 즉, 신경망은 이미지에 포함된 중요한 특징까지도 기계가 합습한다. 이를 종간간 기계학습(End-To-End)라고 할 수 있다. 처음부터 끝까지 입력 데이터에서 목표한 축력 데이터를 사람의 개입 없이 얻을 수 있다.
2. 훈련데이터(Training Data)와 시험데이터(Test Data)
Tensorflow로 러닝을 해본 사람들은 경험 했을 텐데, 처음에 데이터를 렌던으로 훈련데이터와 시험데이터를 분류한 경험이 있을 것이다. 이렇게 나누는 이유는 우리는 학습한 데이터만 인식하고 분류하는 걸 원하지 않고 범용적으로 분류가 되길 원한다. 그렇기 때문에 훈련데이터와 시험데이터를 나눈다.
- 훈련 데이터를 사용하여 최적의 매개변수를 찾는다.
- 시험 데이터를 사용하여 앞에 훈련한 모델의 실력을 평가한다.
+ 범용적이라는 말이 헷갈릴 수도 있다. 다시 말하면, 한 데이터 셋에만 지나치게 최적화 된 상태를 Overfitting 이라고 하고 비범용적이라고 할 수 있다.
3. 손실 함수(Loss Funtion)
신경망학습에서 현재의 상태를 하나의 지표로 표현가능하다. 그 지표를 기준으로 최적의 가중치 매개변수 값을 탐색한다. 신경망 학습에서 사용하는 지표는 손실함수(Loss Function)이다. 그리고 일반적으로 평균 제곱 오차와 교차 엔트로피 오차를 사용한다.
+ 정리하면 손실함수는 신경망 성능이 안 좋은 정도를 나타내며, 수치가 낮을수록 훈력 데이터를 잘 처리하는 것이다.
3.1 평균제곱오차(Mean Squared Error, MSE)
(보통 분류 시 MSE 보다 cross entropy를 많이 사용한다. 그 이유에 대해서는 cross entropy를 블로그에서 검색하보자 참고하자)
먼저 수식을 보면 다음과 같다.
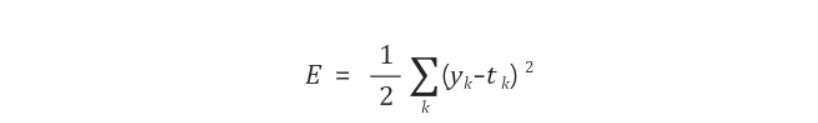
- y : 신경망의 출력(각각의 뉴런의 output)
- t : 정답 레이블
- k : 데이터의 차원 수
t과 t의 예시를 보자. 여기서는 손글씨의 숫자를 알아보는 예시이다. 숫자는 0부터 9까지 있으며, t의 인덱스 값이 숫자라고 판단하고 보면 된다.
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]앞에서 공부를 했다면 y,t가 무슨 말인지 쉽게 알겠지만, 모르는 사람들을 위해서 좀 더 자세하게 적어보겠다. 이론적인 이야기를 먼저 하면 y는 소프트맥스 함수의 출력이다. 그리고 t는 원-핫 인코딩 이라고 한다.
우리가 예시를 든 것은 손글씨로 적은 숫자를 인식하는 것이고, 해결하고자 하는 문제는 적혀진 숫자를 보고 0~9사이의 숫자 중에 어느 것인지를 알아 내는 것이다. y는 인식하려는 이미지에 그려진 내용이 0~9까지 각각이 얼마나 비슷한가를 확률로 나타낸 것이다. 위의 예를 보면 내가 분석하고자 하는 이미지가 0일 확률이 10프로, 1일 확률이 5프로, 2일 확률이 60프로로 이런식으로 알려준다고 생각하면 된다. t는 y에서 가장 높은 확률만 1로 표현하고 나머지를 0으로 표현함으로 컴퓨터가 판단한 숫자는 2라고 알려준다고 생각 하면 될것이다.
+ 사실 이 부분만 디테일하게 적어도 공부할게 많다. 더 궁금한 사람들은 나의 블로그에서 '신경망'을 검색해보면 관련 글들이 있다. 참고하자.
다시 식으로 넘어오면, MSE는 각 데이터의 차원에서의 원소의 출력 값과 정답 레이블의 차를 제곱한 후에 그 총합을 구하는 것이다. 이함수를 사용한 예를 보자.
# 예 1.
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> mean_squared_error(np.array(y), np.array(t))
0.0975000000
# 예 2.
>>> t = [0, 0, 0, 0, 0, 0, 0, 1, 0, 0]
>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> mean_squared_error(np.array(y), np.array(t))
0.5975000000
예1을 보면 판단하려는 이미지에 적힌 숫자가 2일 확률이 가장 높다고 하였고, 두번째 예시는 7인 확률이 가장 높다고 하였다. 상식적으로 봐도 예 1이 더 정확한 것을 알 수 있다. 컴퓨터 기준으로 보면 예1이 정답에 더 가까워 보임을 알 수 있다.
3.2 교차 엔트로피 오차(Cross Entropy Error, CEE)
손실 함수로 MSE 외에도 CEE도 자주 사용한다. 먼저 수식부터 보자.

- log 밑이 e인 자연로그이다
- y : 신경망의 출력
- t : 정답 레이블
정답 레이블이 2라고 해보자. 이때의 신경망 출력이 0.6이라면 교차 엔트로피 오차는 -log0.6 = 0.51 이다. 같은 조건에서 신경망 출력이 0.1이라면 -log0.1 = 2.30이 된다. 즉, 교차 엔트로피 오차는 정답일 떄의 출력이 전체 값을 정하게 된다.
+ 쉽게 말하면 곱하기니까 t의 정답 레이블에서 0인 부분은 곱해도 0이 되므로 1인 부분이 전체 값을 정한다.
아래의 자연로그 그래프를 보자.

포인트는 y의 값이 1에 가까워 질수록 결과값은 작아진다. 특정 인덱스에서 나타내는 특정 숫자인 확률이 클수록 1에 가깝고, 1에 가까울 수록 loss 값이 작아진다. 결과 값이 작을 수록 정답일 가능성이 높다는 것을 아음의 예로 판단 할 수 있다.
#예1
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> cross_entropy_error(np.array(y), np.array(t))
0.51082
#예2
>>> t = [0, 0, 0, 0, 0, 0, 0, 1, 0, 0]
>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> cross_entropy_error(np.array(y), np.array(t))
2.30258
3.3 미니배치학습
훈련 데이터를 보면 보통 60,000 개에서 많게는 수천만개까지도 있을 수 도 있다. 이 많은 데이터를 대상으로 전부 손실함수를 계산하는 것은 현실적이지 않다. 이런 경우 데이터 일부를 추려 전체의 근사치로 이용한다. 신경망 학습에서 훈련데이터로부터 일부만 골라 합습을 하는 것을 미니배치(Mini-Batch)라고 한다. 예를들면 6만장의 훈련 데이터 중에서 100장을 무작위로 뽑아 학습하는 것을 미니배치라고 한다.
우리는 머신러닝 문제를 해결 할 때 훈련데이터에 대한 손실 함수의 값을 구하고, 그 값을 최대한 줄여주는 매개변수를 찾는다. 즉, 우리는 훈련 데이터를 대상으로 손실 함수 값을 구해야한다. 그렇다면 데이터 하나에 대한 손실 함수가 아니라 훈련데이터 전체를 반영한 손실함수의 합을 구하는 방법을 알아보자.
위에서 배운 내용중 교차 엔트로피 오차 수식은 아래와 같다.

위의 식과 다른점은 데이터의 갯수인 N이 포함된 것이다. nk는 n번째 데이터의 k번째 값을 의미한다. 그리고 마지막에 N으로 나눠 정규화를 한다. 이러한 방식으로 진행하면 훈련데이터 개수와 상관없이 통일된 지표를 구할 수 있고 평균 손실 함수를 구할 수 있다.
4. 손실함수(Loss Function)을 쓰는이유
나는 처음으로 손실함수를 접했을 때, 왜 정확도를 안 구하고, loss값을 구할까?라는 질문을 했다. 이러한 의문은 '미분'이라는 역할을 생각해 보면 해결 할 수 있다. 신경망 학습에서는 최적의 매개변수 (가중치와 편향) 값을 탐색할 떄 손실 함수의 값을 가능한 작게 하는 매개변수 값을 찾는다. 이 때 매개변수의 미분을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는과정을 반복하게 된다.
가령 여기에 가상의 신경망이 있고 그 신경망의 어느 한 가중치 매개변수에 주목한다고 할 때 그 가중치 매개변수의 손실함수의 미분이란 가중치 매개변수의 값을 아주 조금 변화 시켰을 때 손실 함수가 어떻게 변하냐의 의미이다. 만약 이 미분 값이 음수라면 그 가중치 매개변수를 양의 방향으로 변화시켜 손실 함수의 값을 줄일 수 있다. 반대로, 이 미분 값이 양수라면 그 가중치 매개변수를 음의 방향으로 변화시켜 손실 함수의 값을 줄일 수 있다. 그러나 미분 값이 0 이라면 가중치 매개변수를 어느 쪽으로 움직여도 손실 함수의 값은 달라지지 않는다. 그래서 그가중치 매개변수의 갱신은 거기서 멈춘다. + 이부분도 신경망 부분에서 자세히 다뤘다.
정리하면, 손실함수는 매개변수의 변화에 연속적으로 변화하지만, 정확도는 매개변수의 변화에 둔감하고, 변화가 있더라도 불연속적으로 변화하기 때문에 미분이 불가능하다. 미분이 안되면 최적화를 할 수 없어서 정확도가 아닌 손실 함수를 지표를 삼아 학습을 하는 것이다.
'인공지능(Artificial Intelligence) > 딥러닝(Deep Learning)' 카테고리의 다른 글
| [Deep learning] Activation Function(활성화 함수) 개념 (0) | 2020.09.25 |
|---|
- Total
- Today
- Yesterday
- nextjs autoFocus
- next.config.js
- Queue
- error:0308010C:digital envelope routines::unsupported
- JavaScript
- 자연어처리
- DFS
- 클라우데라
- Express
- react autoFocus
- logout
- vuejs
- TensorFlow
- Vue
- NextJS
- typescript
- 자료구조
- django
- useState
- useHistory 안됨
- Python
- pandas
- mongoDB
- Deque
- BFS
- nodejs
- read_csv
- login
- UserCreationForm
- react
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
